Assignment A01:Linear regression

Jul 9, 2021 · 14 min read  ·
Share on:
Assignment A01:Linear regression

Diamonds

The diamonds dataset that we will use in this application exercise consists of prices and quality information.

The variables in the diamonds dataset are

  1. price: price in US dollars
  2. carat: weight of the diamond
  3. cut: quality of the cut (Fair, Good, Very Good, Premium, Ideal)
  4. color: diamond color, from J (worst) to D (best)
  5. clarity: a measurement of how clear the diamond is, from I1 (worst), SI1, SI2, VS1, VS2, VVS1, VVS2, to IF (best)

Load required packages

library(QuantPsyc)
## Loading required package: boot
## Loading required package: MASS
## 
## Attaching package: 'QuantPsyc'
## The following object is masked from 'package:base':
## 
##     norm
library(MASS)
library(dplyr)
## 
## Attaching package: 'dplyr'
## The following object is masked from 'package:MASS':
## 
##     select
## The following objects are masked from 'package:stats':
## 
##     filter, lag
## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union
library(data.table)
## 
## Attaching package: 'data.table'
## The following objects are masked from 'package:dplyr':
## 
##     between, first, last
library(tidyr)
library(ggplot2)
library(GGally)
## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2
library(gridExtra)
## 
## Attaching package: 'gridExtra'
## The following object is masked from 'package:dplyr':
## 
##     combine
library(mosaic)
## Registered S3 method overwritten by 'mosaic':
##   method                           from   
##   fortify.SpatialPolygonsDataFrame ggplot2
## 
## The 'mosaic' package masks several functions from core packages in order to add 
## additional features.  The original behavior of these functions should not be affected by this.
## 
## Attaching package: 'mosaic'
## The following object is masked from 'package:Matrix':
## 
##     mean
## The following object is masked from 'package:ggplot2':
## 
##     stat
## The following objects are masked from 'package:dplyr':
## 
##     count, do, tally
## The following object is masked from 'package:boot':
## 
##     logit
## The following objects are masked from 'package:stats':
## 
##     binom.test, cor, cor.test, cov, fivenum, IQR, median, prop.test,
##     quantile, sd, t.test, var
## The following objects are masked from 'package:base':
## 
##     max, mean, min, prod, range, sample, sum

load data

let us check the structure of the dataset.

diamonds <- read.csv("MBA6636_SM21_Professor_Proposes_Data.csv")   #read diamonds file
head(diamonds)    #display some of the data
##   Carat Colour Clarity Cut Certification Polish Symmetry Price Wholesaler
## 1  0.92      I     SI2   G           AGS      V        V  3000          1
## 2  0.92      I     SI2   V           AGS      G        G  3000          1
## 3  0.82      F     SI2   I           GIA      X        X  3004          1
## 4  0.81      G     SI1   I           GIA      X        V  3004          1
## 5  0.90      J     VS2   V           GIA      V        V  3006          1
## 6  0.87      F     SI2   I           AGS      G        V  3007          1

Another function that is very useful for quickly taking a peek at a dataset is str. This function compactly displays the internal structure of an R object.

str(diamonds)  #data frame by observations and variables
## 'data.frame':    441 obs. of  9 variables:
##  $ Carat        : num  0.92 0.92 0.82 0.81 0.9 0.87 0.8 0.84 0.8 0.8 ...
##  $ Colour       : chr  "I" "I" "F" "G" ...
##  $ Clarity      : chr  "SI2" "SI2" "SI2" "SI1" ...
##  $ Cut          : chr  "G" "V" "I" "I" ...
##  $ Certification: chr  "AGS" "AGS" "GIA" "GIA" ...
##  $ Polish       : chr  "V" "G" "X" "X" ...
##  $ Symmetry     : chr  "V" "G" "X" "V" ...
##  $ Price        : int  3000 3000 3004 3004 3006 3007 3008 3010 3012 3012 ...
##  $ Wholesaler   : int  1 1 1 1 1 1 1 1 1 1 ...

The output above tells us that there are observations and variables in the dataset. The variable name are listed, along with their type and the first few observations of each variable.

More about the dataset

Before we go any further with the analysis, let us first understand what each column in the dataset means. And who are we going to rely on to help us with that? The American Gemological Institute (GIA). So, let’s decipher the 4Cs and other fields in the dataset.

  1. Carat weight: Represents the weight of the diamond. Bigger, the better (if other factors are held constant).

  2. Clarity: Refers to the absence of inclusions and blemishes. The clearer the diamond, the better the diamond, expensive the diamond (Other factors held constant).

  3. Color: Color refers to the absence of color in diamonds.

  4. Cut: Based on various dimensions, a diamond is assigned a cut rating or grade. This ranges from Excellent to Poor. Our dataset has the following cut ratings: Fair < Good < Very Good < Premium < Ideal Better the cut rating, expensive the diamond (other factors held constant).

  5. Certification, polish, Symmetry, Price: These are physical dimensions of the diamond.

summary(diamonds)
##      Carat           Colour            Clarity              Cut           
##  Min.   :0.0900   Length:441         Length:441         Length:441        
##  1st Qu.:0.3000   Class :character   Class :character   Class :character  
##  Median :0.8100   Mode  :character   Mode  :character   Mode  :character  
##  Mean   :0.6693                                                           
##  3rd Qu.:1.0100                                                           
##  Max.   :1.5800                                                           
##  NA's   :1                                                                
##  Certification         Polish            Symmetry             Price     
##  Length:441         Length:441         Length:441         Min.   : 160  
##  Class :character   Class :character   Class :character   1st Qu.: 520  
##  Mode  :character   Mode  :character   Mode  :character   Median :2169  
##                                                           Mean   :1717  
##                                                           3rd Qu.:3012  
##                                                           Max.   :3145  
##                                                           NA's   :1     
##    Wholesaler   
##  Min.   :1.000  
##  1st Qu.:2.000  
##  Median :2.000  
##  Mean   :2.318  
##  3rd Qu.:3.000  
##  Max.   :3.000  
##  NA's   :1

Exploring variables individually

We will investigate and visualise the distributions of the variables in this dataset. This is also referred to as univariate analysis.

First, variable classification:

  • Numerical variables are classified as continuous or discrete depending on whether they can take on an infinite number of values or only non-negative whole numbers.
  • If the variable is categorical, we can tell if it is ordinal by whether or not the levels are ordered naturally.

Investigating numerical data We emphasise the following points when describing the shapes of numerical distributions:

  • shape:
  • right-skewed, left-skewed, symmetric (skew is to the side of the longer tail)
  • unimodal, bimodal, multimodal, uniform
  • center: mean (mean), median (median), mode (not always useful)
  • spead: range (range), standard deviation (sd), inter-quartile range (IQR)
  • unusal observations

To calculate the mean, median, SD, variance, five-number summary, IQR, minimum, maximum of the price variable in the diamonds dataset.

The mosaic command favstats, allows us to compute all of this information (and more) at once.

favstats(~Price, data=diamonds)
##  min  Q1 median     Q3  max     mean       sd   n missing
##  160 520   2169 3012.5 3145 1716.739 1175.689 440       1

find the mean price of diamonds by quality of cut

mean(Price ~ Cut , data=diamonds)
##                 F        G        I        V        X 
##       NA 2455.220 2046.020 1731.767 1178.103 1658.013
median(Price ~ Cut , data=diamonds)
##             F      G      I      V      X 
##     NA 2516.0 2452.0 2175.5  531.0 2149.0
sd(Price ~ Cut , data=diamonds)
##                   F         G         I         V         X 
##        NA  593.2224 1123.5260 1244.0412 1145.8465 1168.4052
var(Price ~ Cut, data=diamonds)
##                   F         G         I         V         X 
##        NA  351912.8 1262310.6 1547638.6 1312964.3 1365170.6
min(Price ~ Cut, data=diamonds)
##       F   G   I   V   X 
##  NA 468 160 160 160 160
max(Price ~ Cut , data=diamonds)
##         F    G    I    V    X 
##   NA 3138 3145 3139 3091 3142
favstats(Price ~ Cut , data=diamonds)
##   Cut min   Q1 median   Q3  max     mean        sd   n missing
## 1      NA   NA     NA   NA   NA      NaN        NA   0       1
## 2   F 468 2192 2516.0 2780 3138 2455.220  593.2224  59       0
## 3   G 160  547 2452.0 3057 3145 2046.020 1123.5260  49       0
## 4   I 160  520 2175.5 3031 3139 1731.767 1244.0412  86       0
## 5   V 160  519  531.0 3000 3091 1178.103 1145.8465  97       0
## 6   X 160  520 2149.0 2745 3142 1658.013 1168.4052 149       0

The distribution of each cuts.

diamonds %>%
  ggplot(aes(x=(Price))) +
  geom_histogram(stat="bin",binwidth= 500) +
  facet_wrap(~Cut, scales = "free")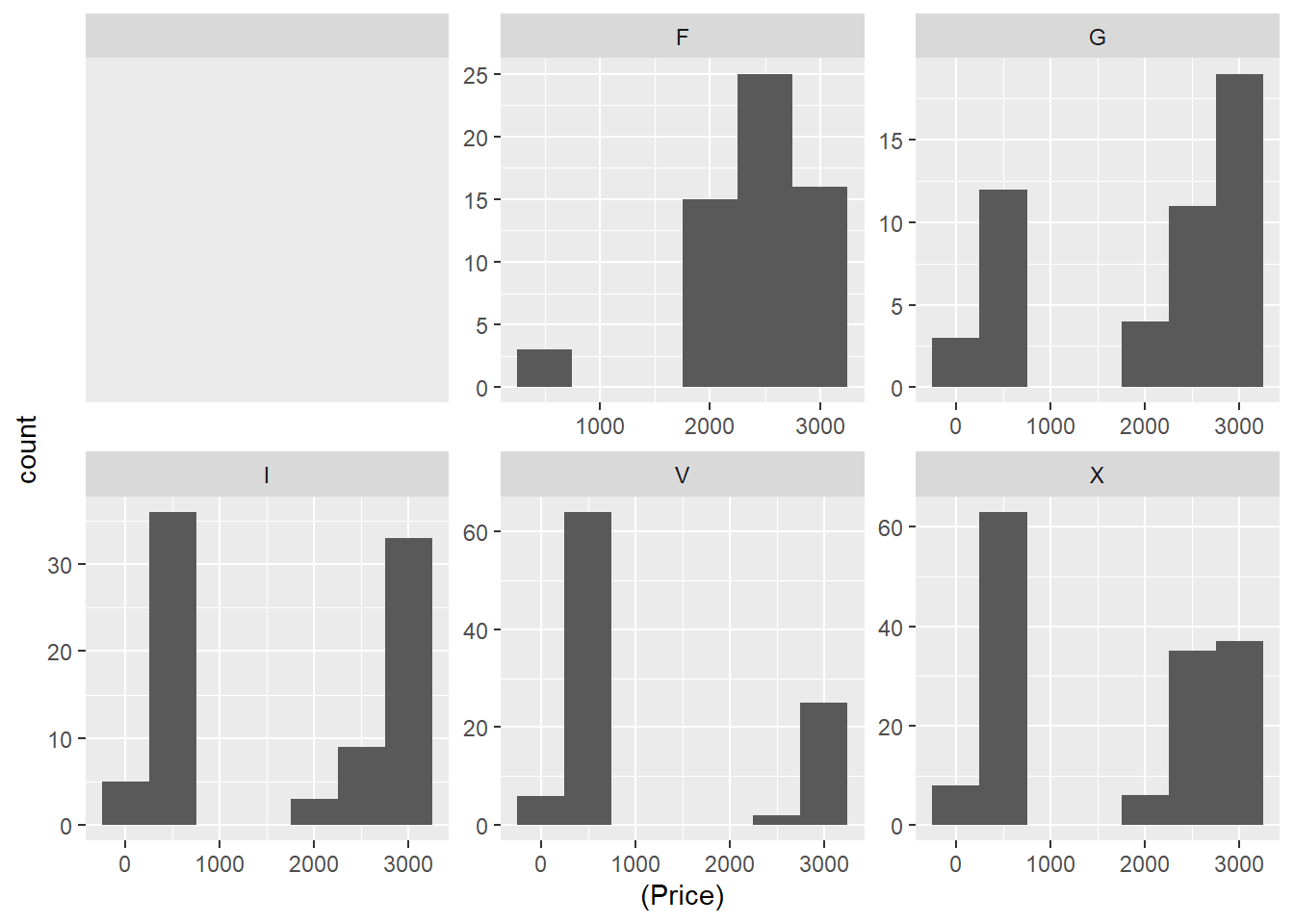

Graphical Display of Data

Histogram of the carat variable:

histogram(~Carat, data=diamonds)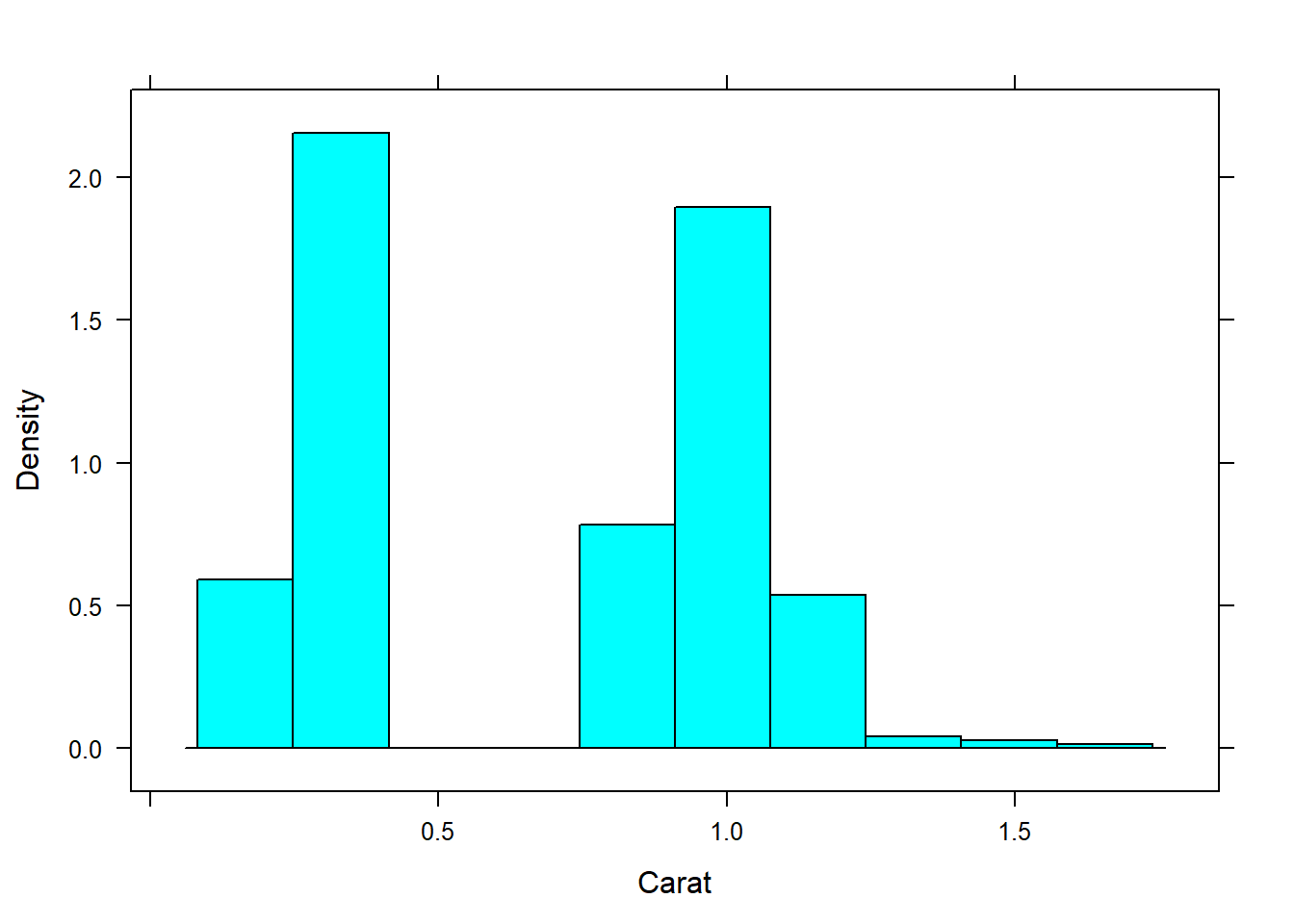

Adjust the binwidth of the histogram:

histogram(~Carat, data=diamonds, width = 0.1)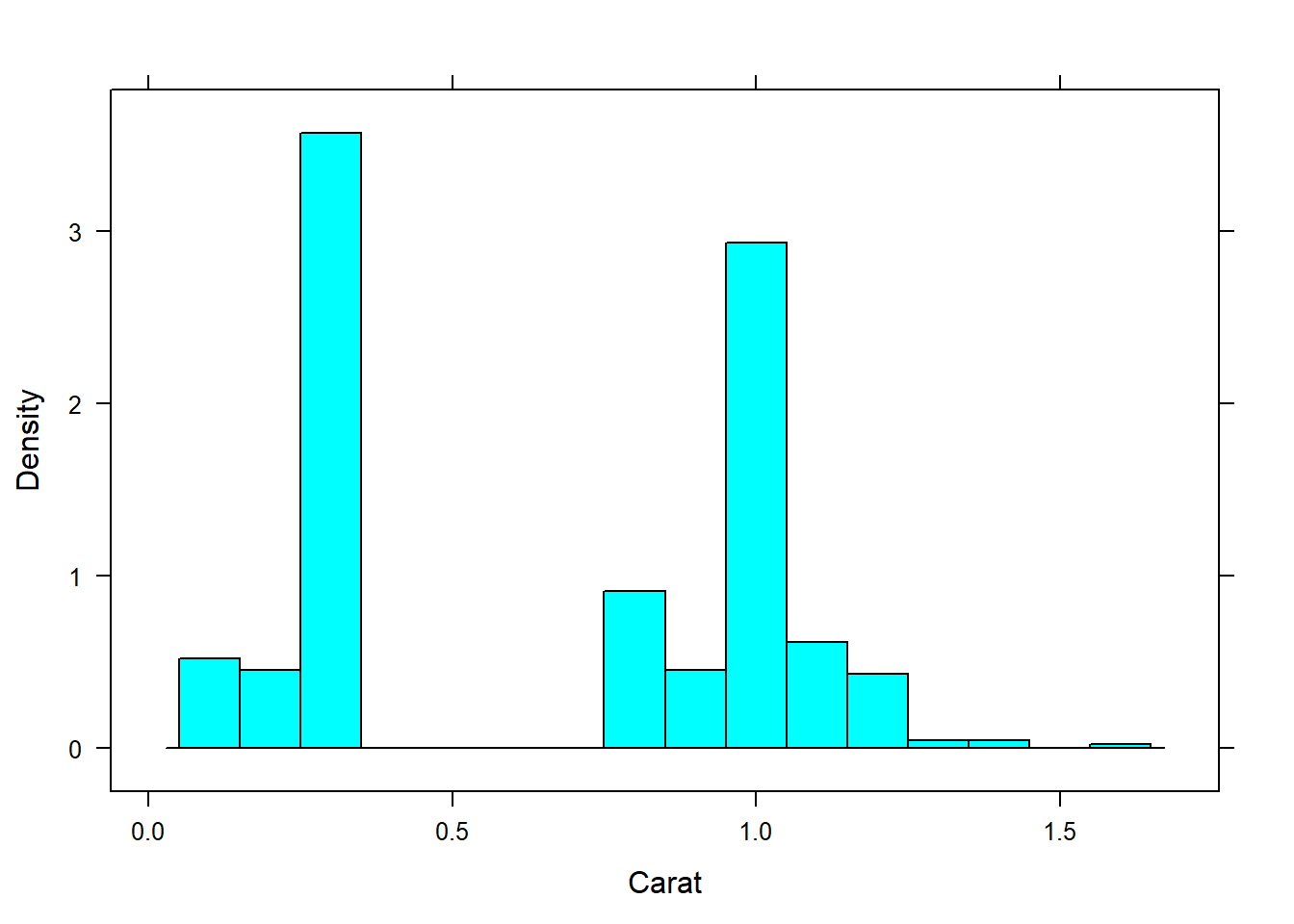

histogram(~Carat, data=diamonds, width = 0.01)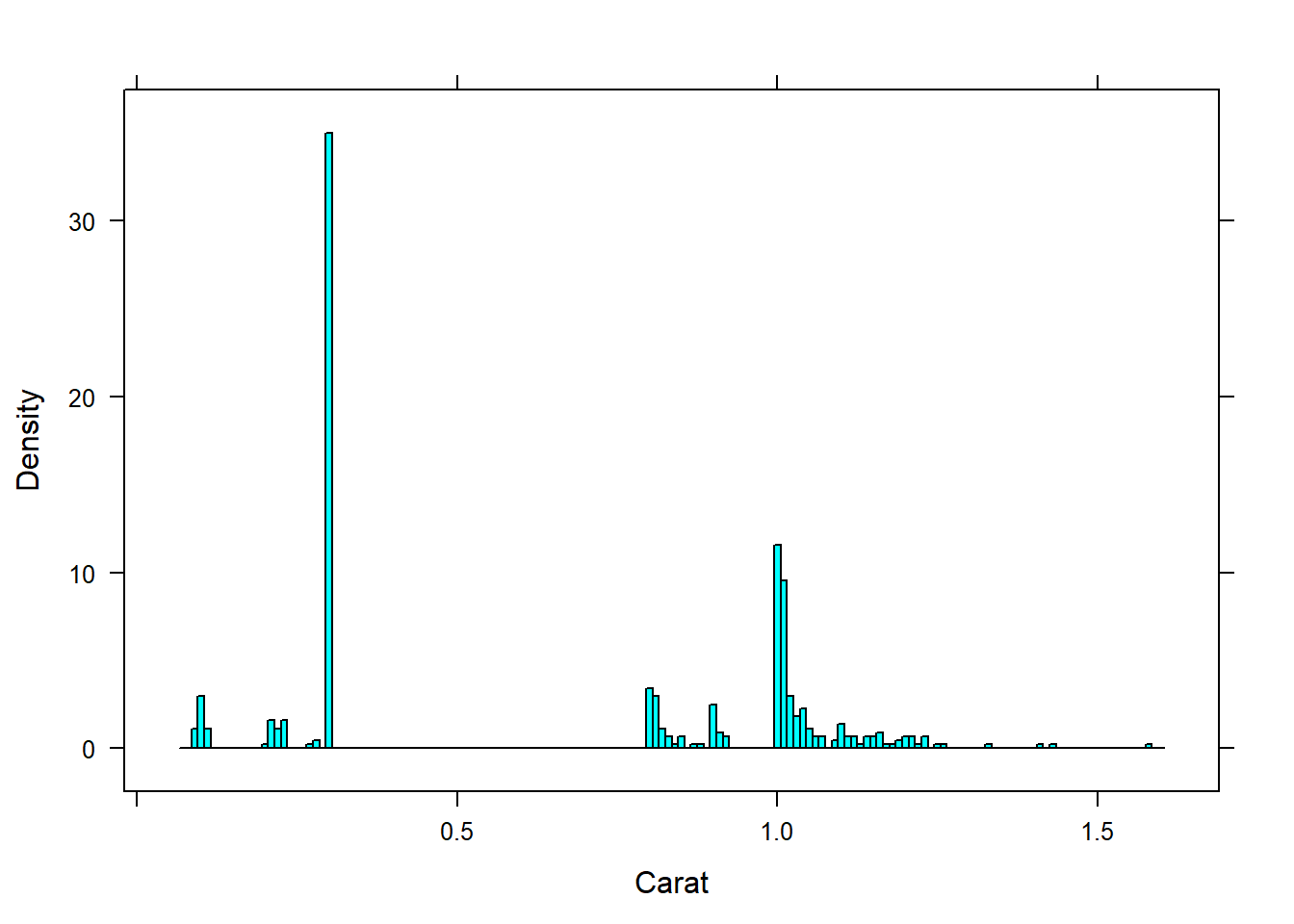

Adjust the number of intervals:

histogram(~Carat, data=diamonds, nint = 50)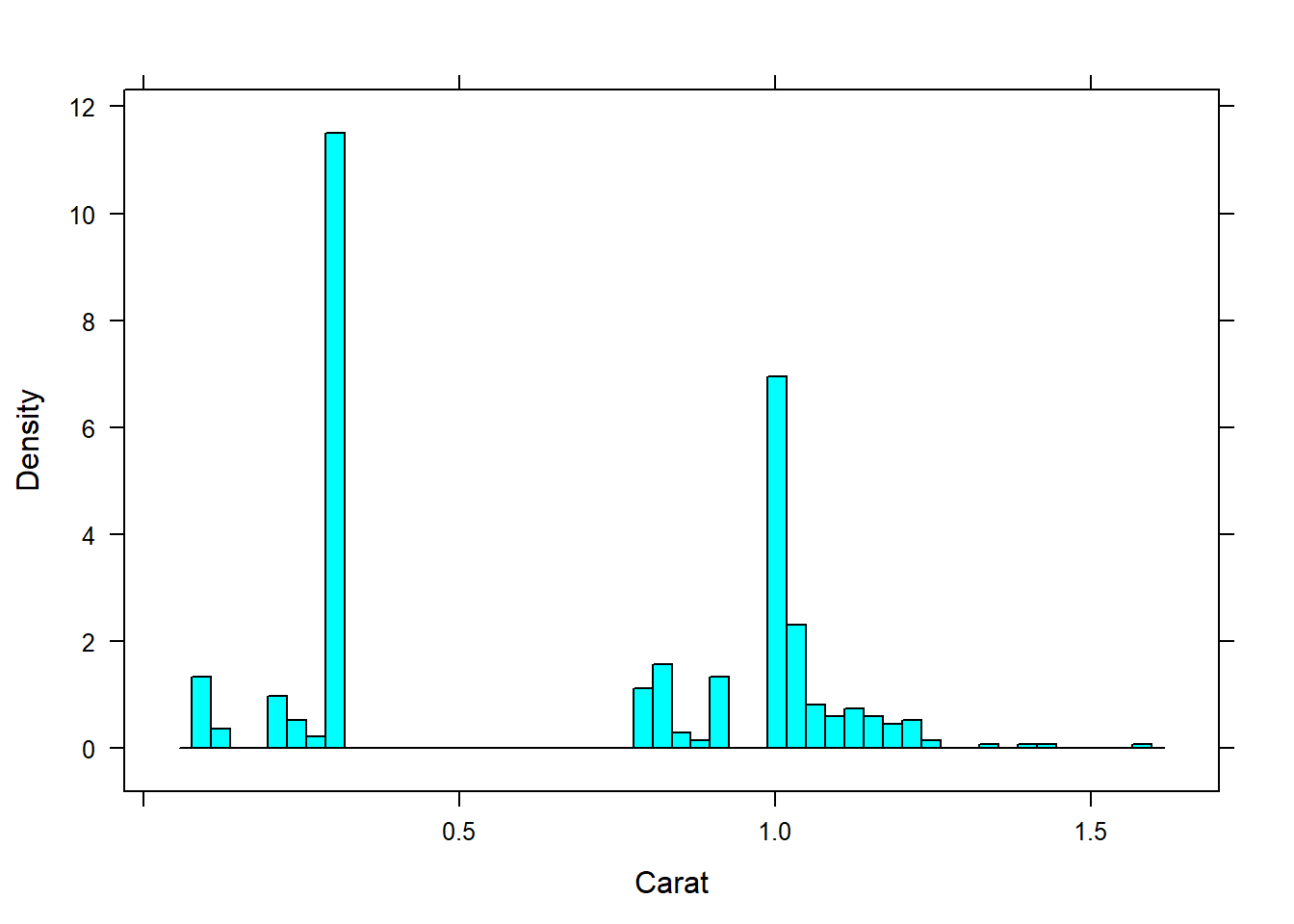

Boxplots:

bwplot(Clarity ~ Price, data=diamonds)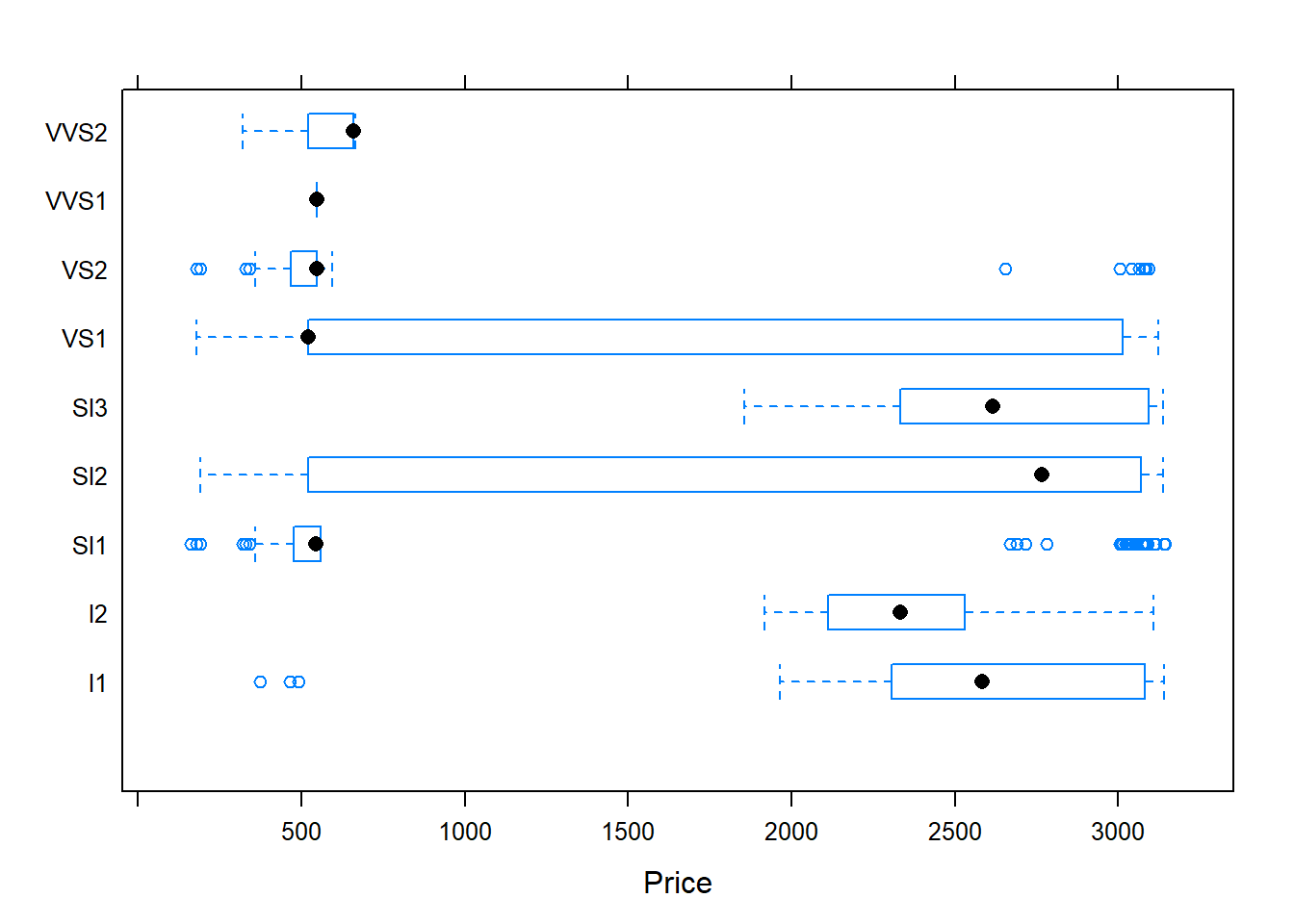

Scatterplots:

Scatterplot between carat and price of diamonds:

qplot(Carat, Price, data=diamonds)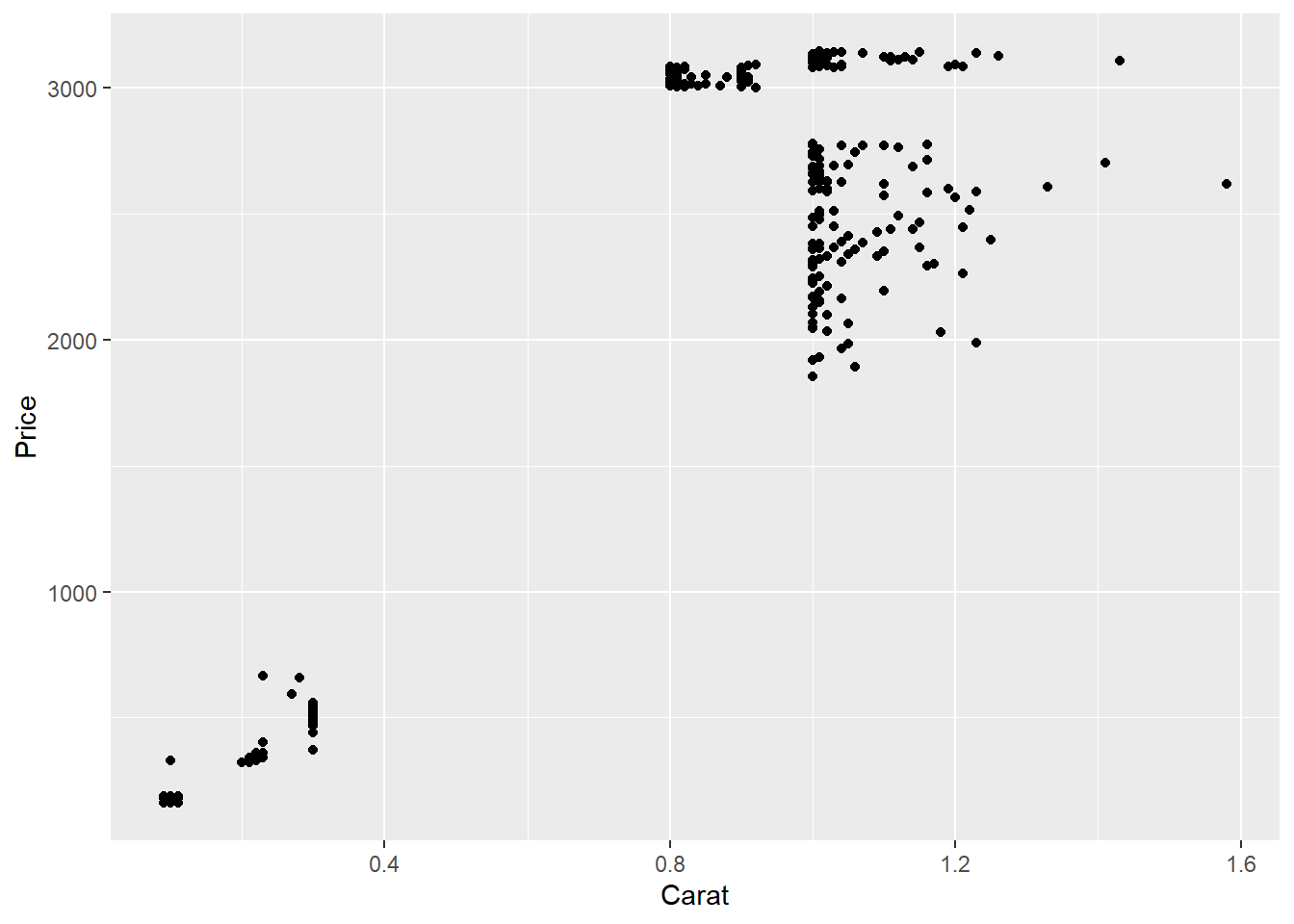

Relationship of Price and Cut

Through a box plot, we observe that the highest price diamonds are premium cut, lowest price diamonds are ideal cut.

dim(diamonds)
## [1] 441   9
samp_index = sample(1:nrow(diamonds), 30, replace = FALSE) # Creating a random sample to look at the data set.
samp_index
##  [1]  63 191  10 311 211 213 171 304 403 293 382 369 109  12  96 406 298 192 285
## [20] 116 437 367 132 355  75 161 215 377 425 145
diamonds[samp_index,]
##     Carat Colour Clarity Cut Certification Polish Symmetry Price Wholesaler
## 63   1.00      K      I2   F           GIA      V        V  1918          2
## 191  1.01      E      I1   X           EGL      G        G  2511          2
## 10   0.80      D     SI2   V           GIA      V        X  3012          1
## 311  0.30      I     SI1   I           GIA      V        V   493          3
## 211  1.01      I      I1   X           GIA      V        G  2651          2
## 213  1.00      L     VS2   F           GIA      G        G  2655          2
## 171  1.01      J     SI2   I           EGL      V        X  3139          2
## 304  0.30      D      I1   X           GIA      V        V   490          3
## 403  0.30      H     SI1   X           GIA      G        G   547          3
## 293  0.30      J     SI1   G           GIA      X        X   466          3
## 382  0.30      I     SI1   I           GIA      V        V   531          3
## 369  0.30      J     VS1   V           GIA      V        V   520          3
## 109  1.15      J      I1   F           EGL      G        G  2368          2
## 12   0.83      G     SI2   I           GIA      X        X  3014          1
## 96   1.00      J     SI3   F           EGL      G        G  2310          2
## 406  0.30      H     SI1   V           GIA      X        V   547          3
## 298  0.30      I     SI2   I           GIA      X        X   476          3
## 192  1.22      K      I1   F           EGL      V        G  2516          2
## 285  0.28      E    VVS2   X           GIA      V        X   658          3
## 116  1.05      I      I1   F           GIA      G        G  2413          2
## 437  0.30      H     SI1   G           GIA      V        V   559          3
## 367  0.30      J     VS1   V           GIA      V        V   520          3
## 132  1.02      K     VS2   I           EGL      X        X  3093          2
## 355  0.30      I     SI1   F           GIA      G        V   520          3
## 75   1.00      H     SI3   F           EGL      F        F  2101          2
## 161  1.02      I     SI3   X           EGL      G        G  3130          2
## 215  1.01      K     SI1   F           EGL      V        G  2668          2
## 377  0.30      J     VS1   I           GIA      V        V   520          3
## 425  0.30      I     VS2   V           GIA      V        V   547          3
## 145  1.01      F     SI3   I           EGL      V        G  3111          2
str(diamonds$Carat)
##  num [1:441] 0.92 0.92 0.82 0.81 0.9 0.87 0.8 0.84 0.8 0.8 ...
levels(diamonds$Carat)
## NULL
plot(diamonds$Carat)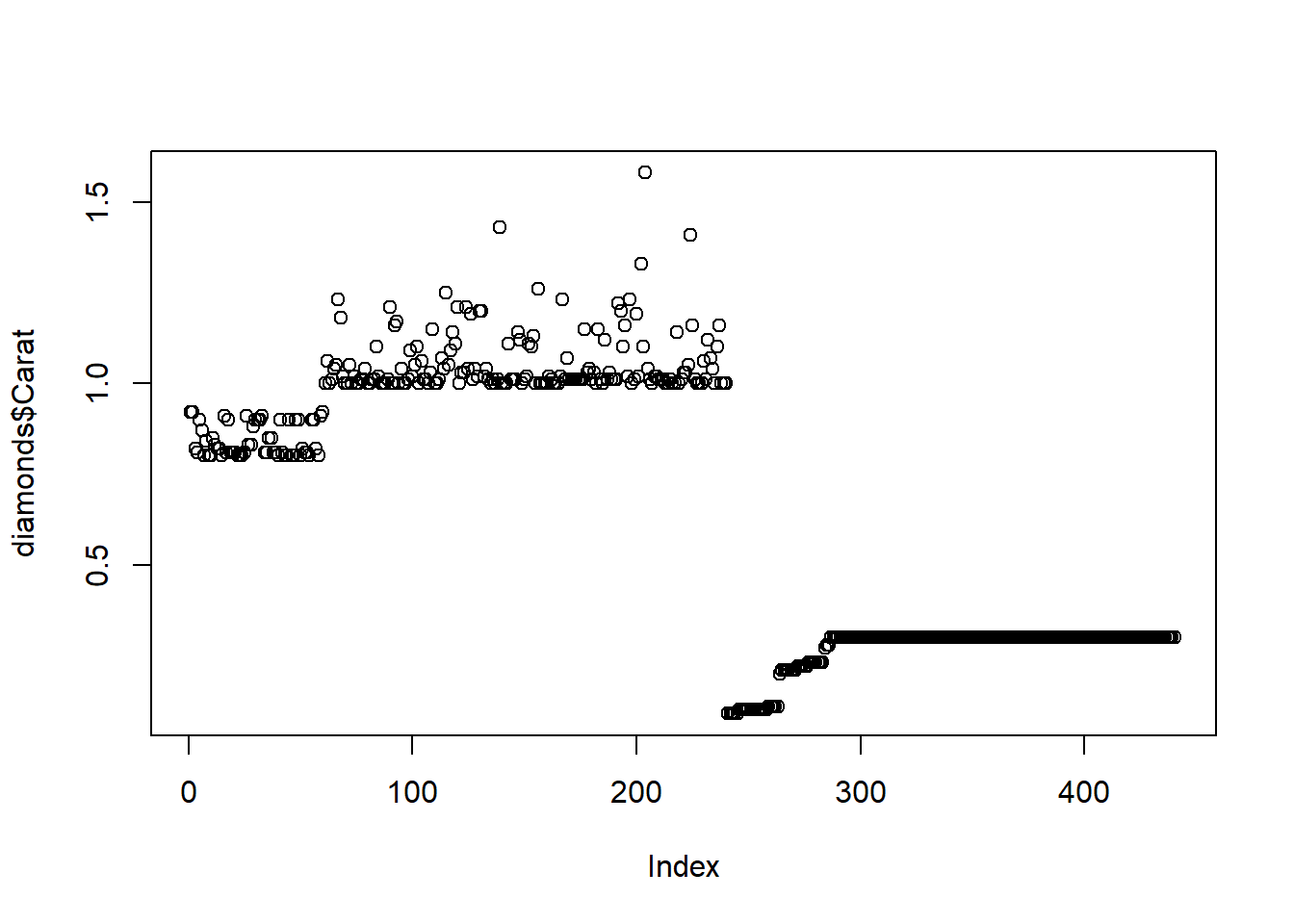

Lets take a closer look at the other ordinal factor variables.

ggplot(diamonds, aes(factor(Cut), Price, fill=Cut)) + geom_boxplot() + ggtitle("Diamond Price according Cut") + xlab("Type of Cut") + ylab("Diamond Price in US Dollars")
## Warning: Removed 1 rows containing non-finite values (stat_boxplot).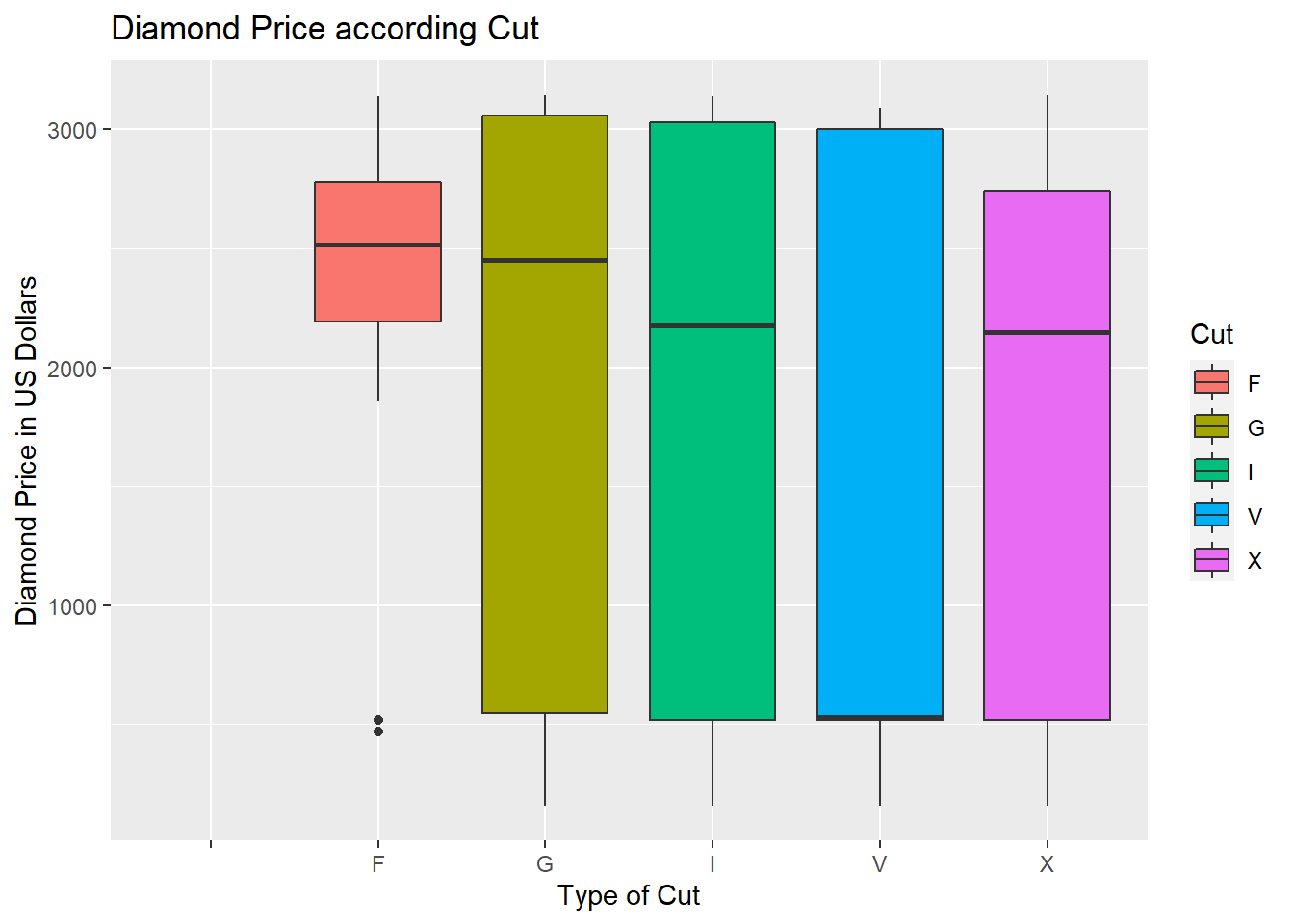

Price vs Categorical Variables: Clarity, Cut, Color

We can see that these three variables all have a relationship with Price by plotting the categorical variables as colour. We can deduce from this that these three variables are important in predicting price, so we’ll include them as features in our next prediction model.

par(mfrow=c(1,3))
diamonds %>%
  ggplot(aes(log(Price),log(Carat), col= Clarity))+
  geom_point()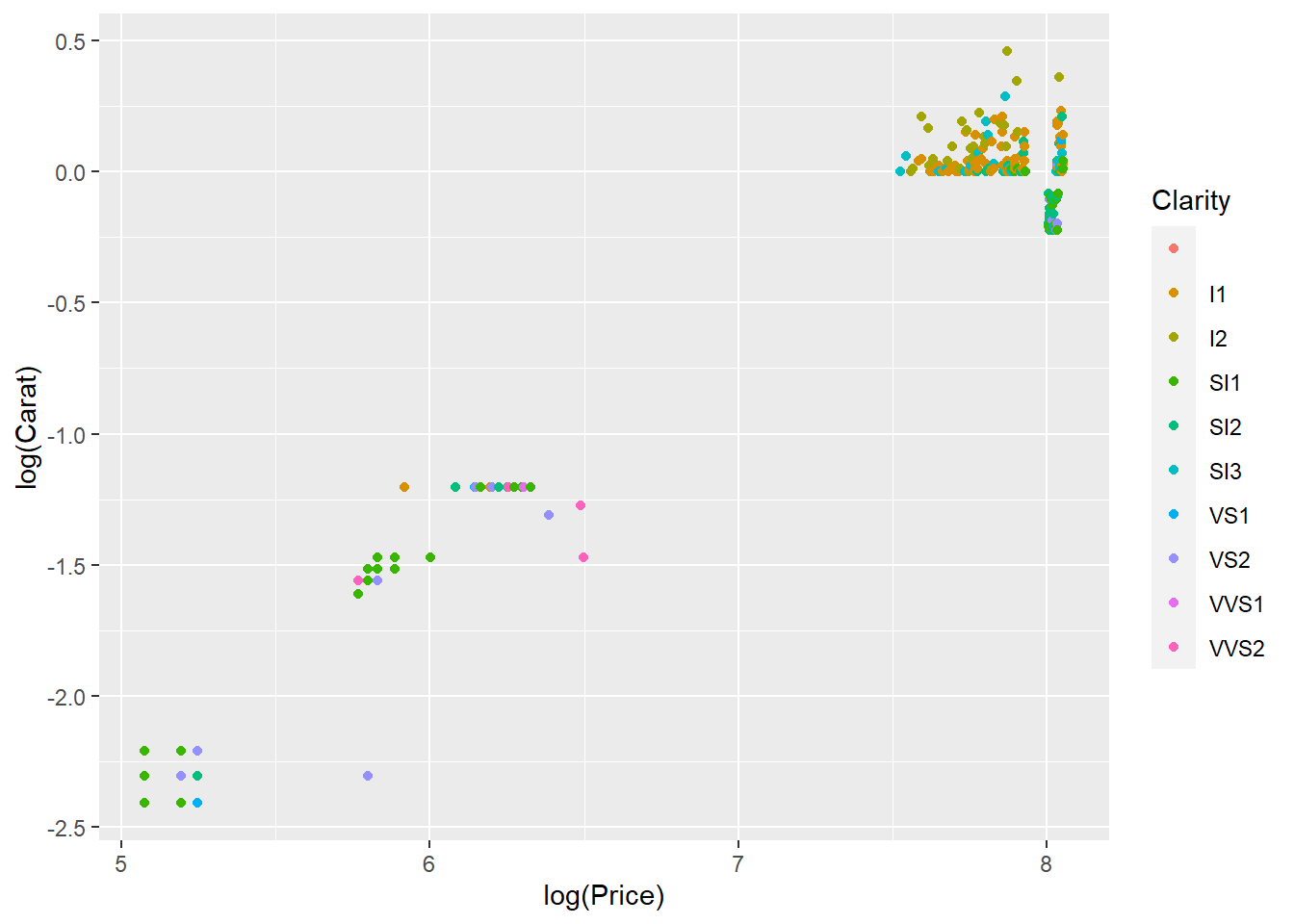

diamonds %>%
  ggplot(aes(log(Price),log(Carat), col= Cut))+
  geom_point()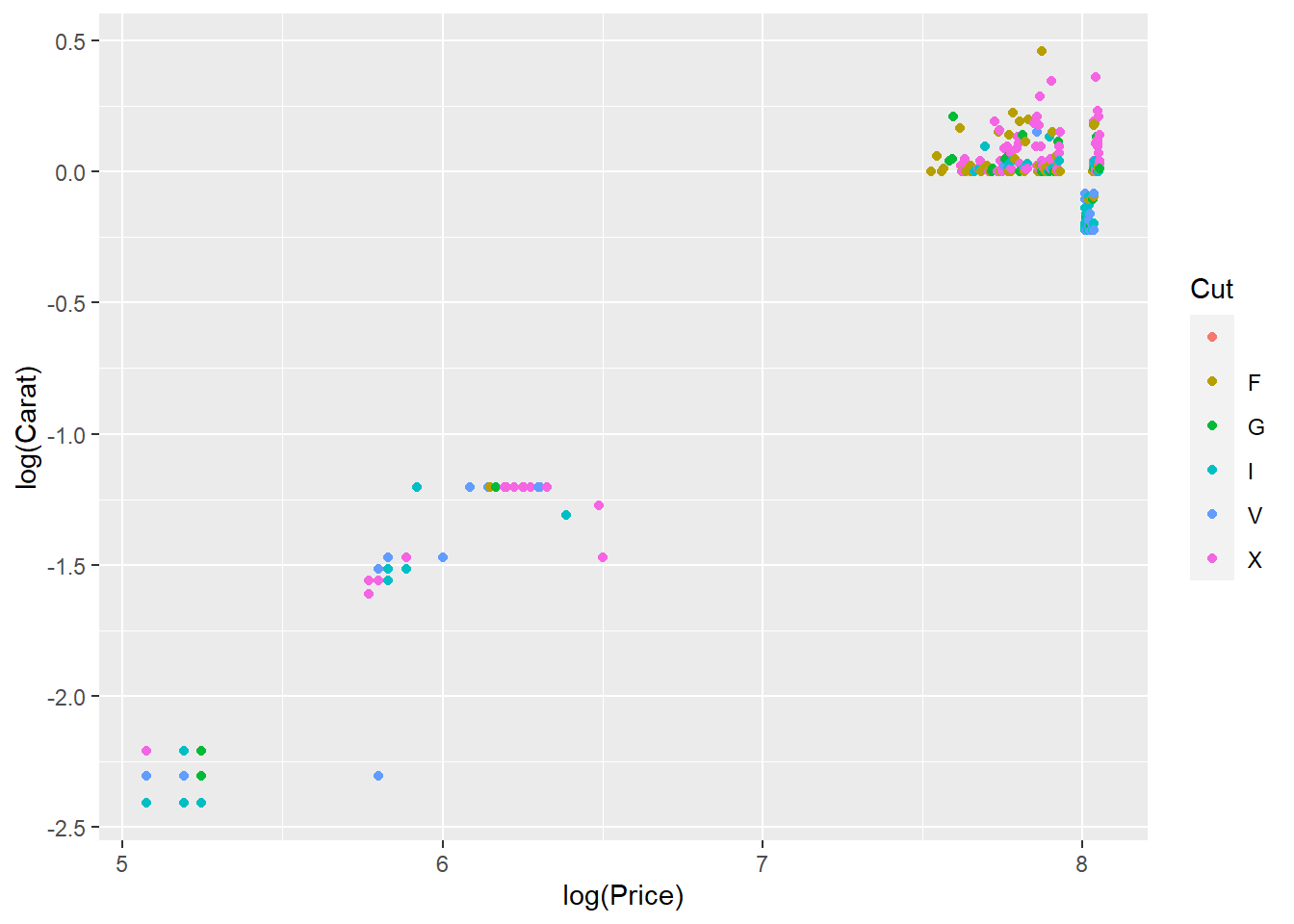

diamonds %>%
  ggplot(aes(log(Price),log(Carat), col= Colour))+
  geom_point()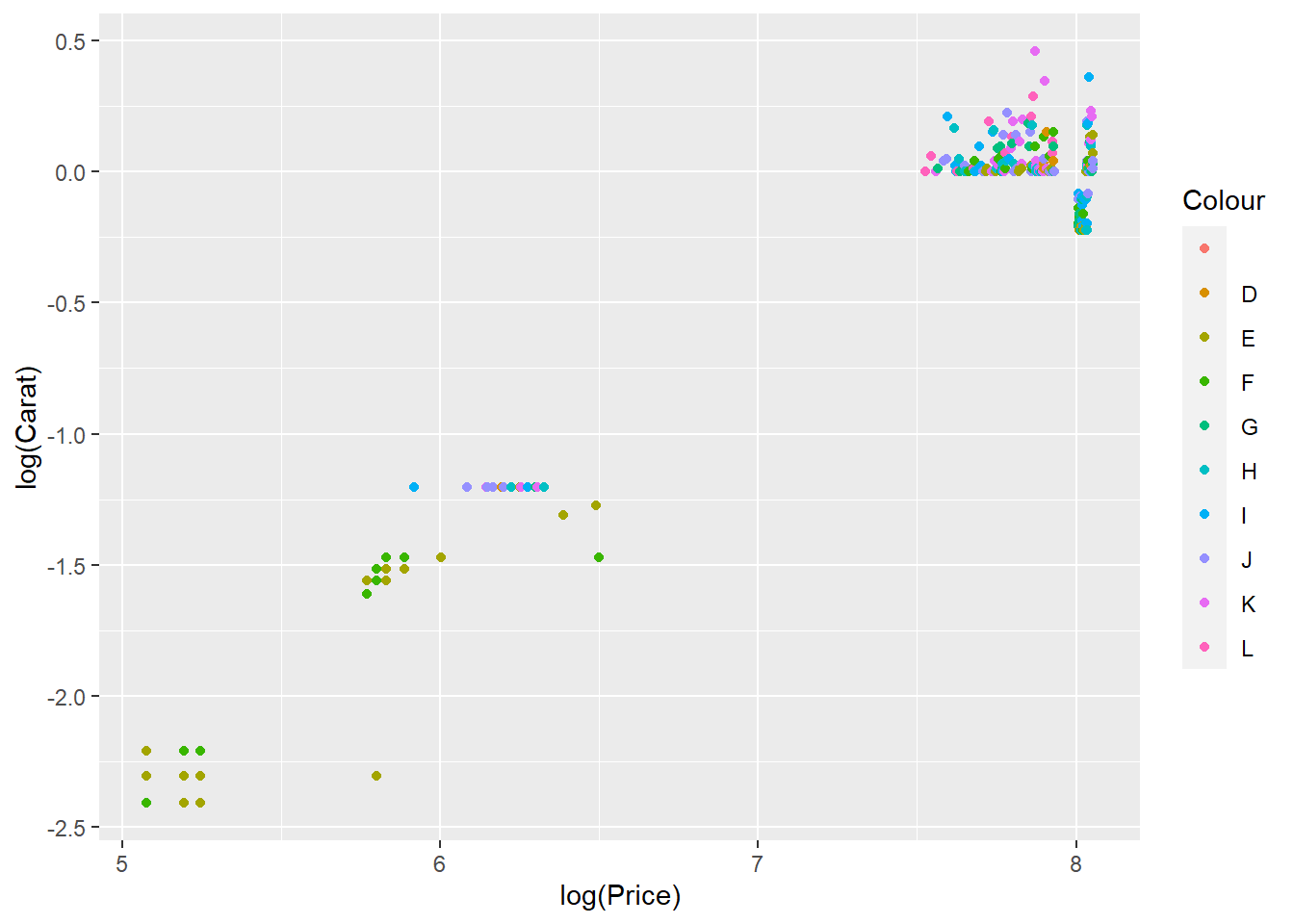

Exploring categorical data

Summarize cuts of diamonds. Since this is a categorical variable we use tables. To create the table, first group by the levels of the cut variable, and then summarize the counts of diamonds in each level.

  • Frequency table:
diamonds %>%
  group_by(Cut) %>%
  summarise(counts = n())
## # A tibble: 6 x 2
##   Cut   counts
##   <chr>  <int>
## 1 ""         1
## 2 "F"       59
## 3 "G"       49
## 4 "I"       86
## 5 "V"       97
## 6 "X"      149
  • Proportions table: divide the counts in each level by the number of rows (observations) in the diamonds variable:
diamonds %>%
  group_by(Cut) %>%
  summarise(counts = n() / nrow(diamonds))
## # A tibble: 6 x 2
##   Cut    counts
##   <chr>   <dbl>
## 1 ""    0.00227
## 2 "F"   0.134  
## 3 "G"   0.111  
## 4 "I"   0.195  
## 5 "V"   0.220  
## 6 "X"   0.338

What type of variable is color? Are all colors of diamonds represented in the dataset? Which color is most prominently represented in the dataset?

A useful representation for categorical variables is a bar plot.

ggplot(data = diamonds, aes(x = Colour)) +
  geom_bar()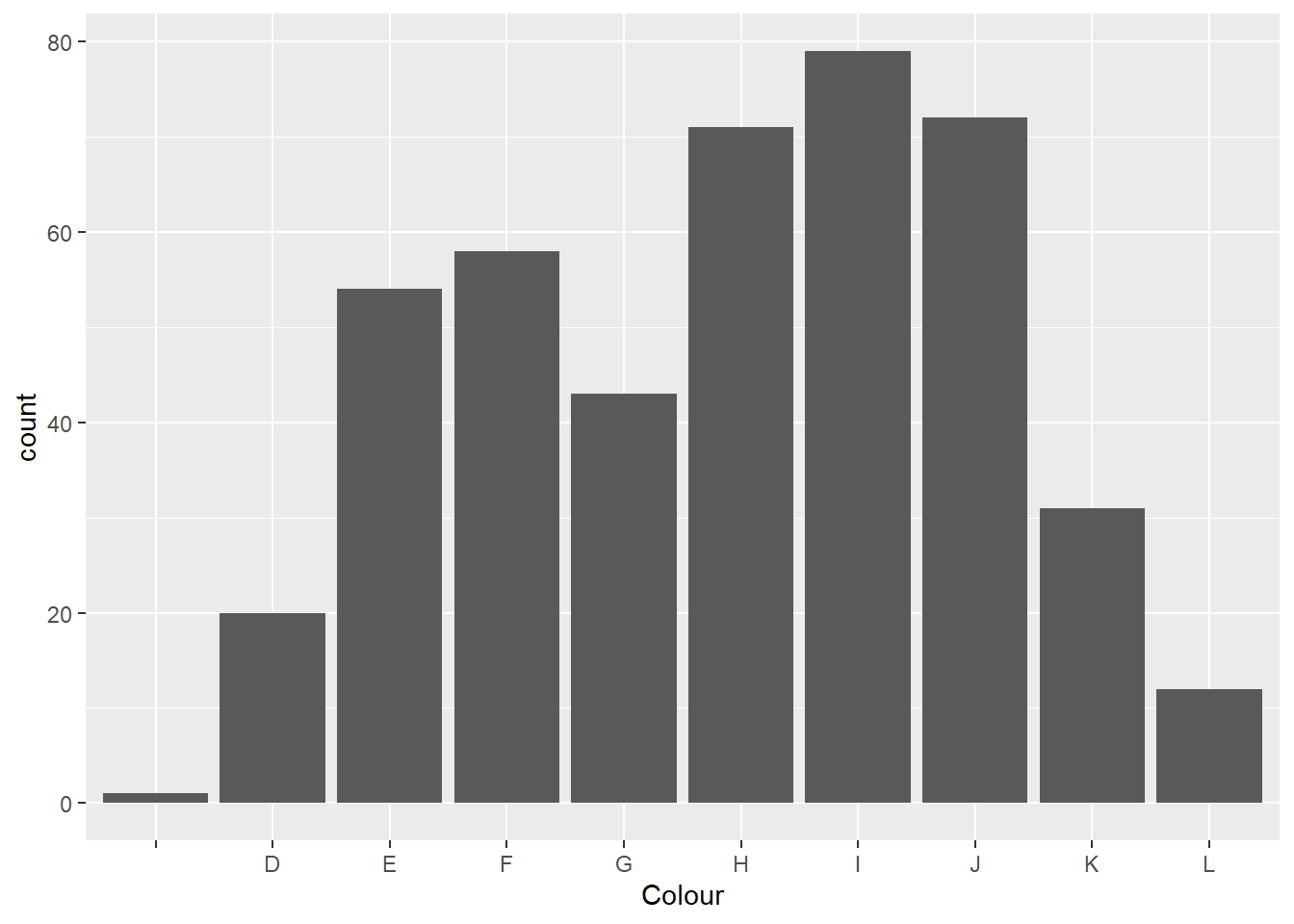

Bivariate Analysis:

We are familiar with the individual variables in the dataset, we can start evaluating relationships between them.

Adding another variable to a histogram:

Let’s make a histogram of the depths of diamonds, with binwidth of 0.2%, and adding another variable i.e cut, to the visualization. We can do this either using an aesthetic or a facet:

  • Using aesthetics: Use different colors to fill in for different cuts.
ggplot(data = diamonds, aes(x = Carat, fill = Cut)) +
  geom_histogram(binwidth = 0.2)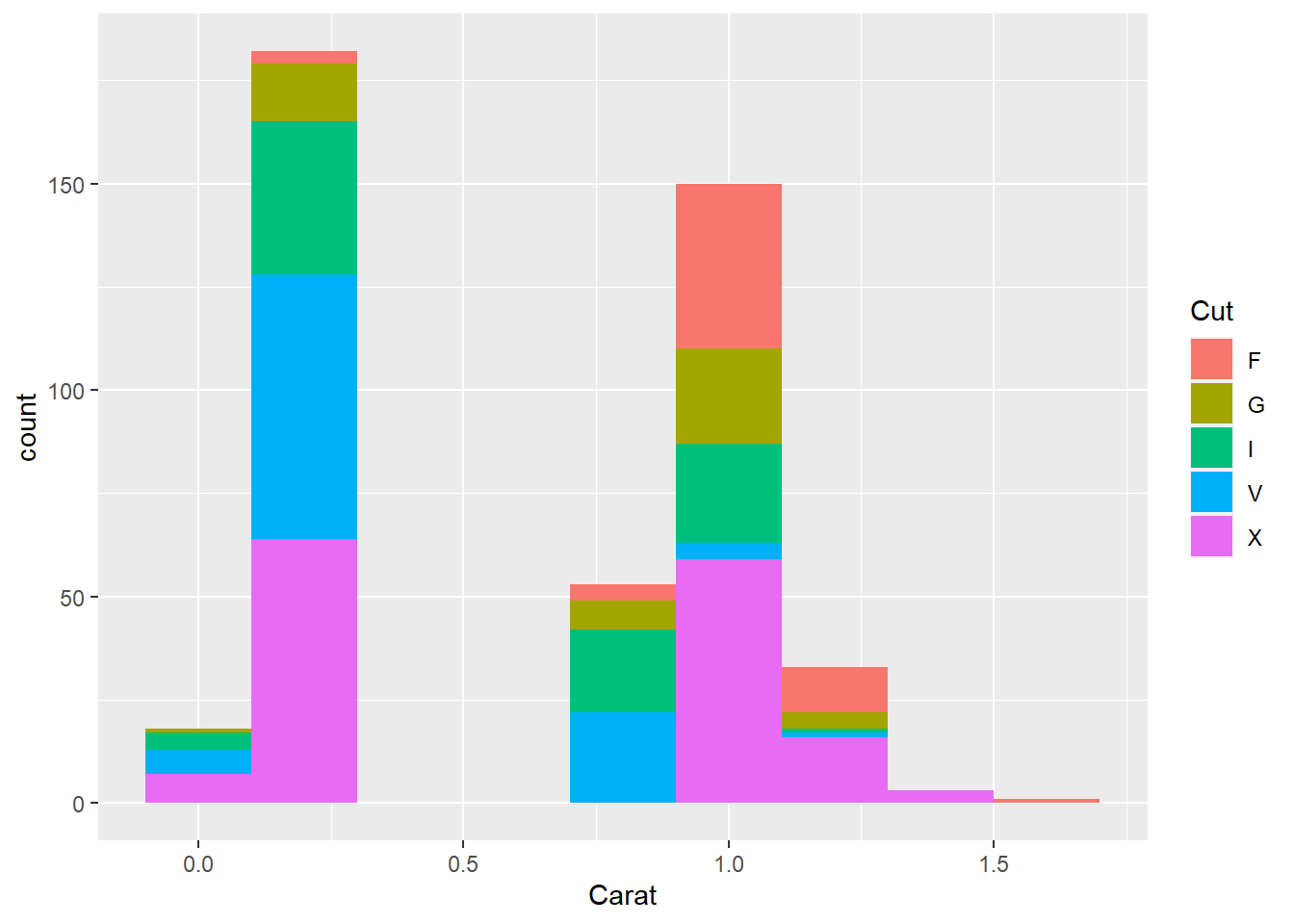

  • Using facets: Split into different plots for different cuts.
ggplot(data = diamonds, aes(x = Carat)) +
  geom_histogram(binwidth = 0.2) +
  facet_wrap(~ Cut)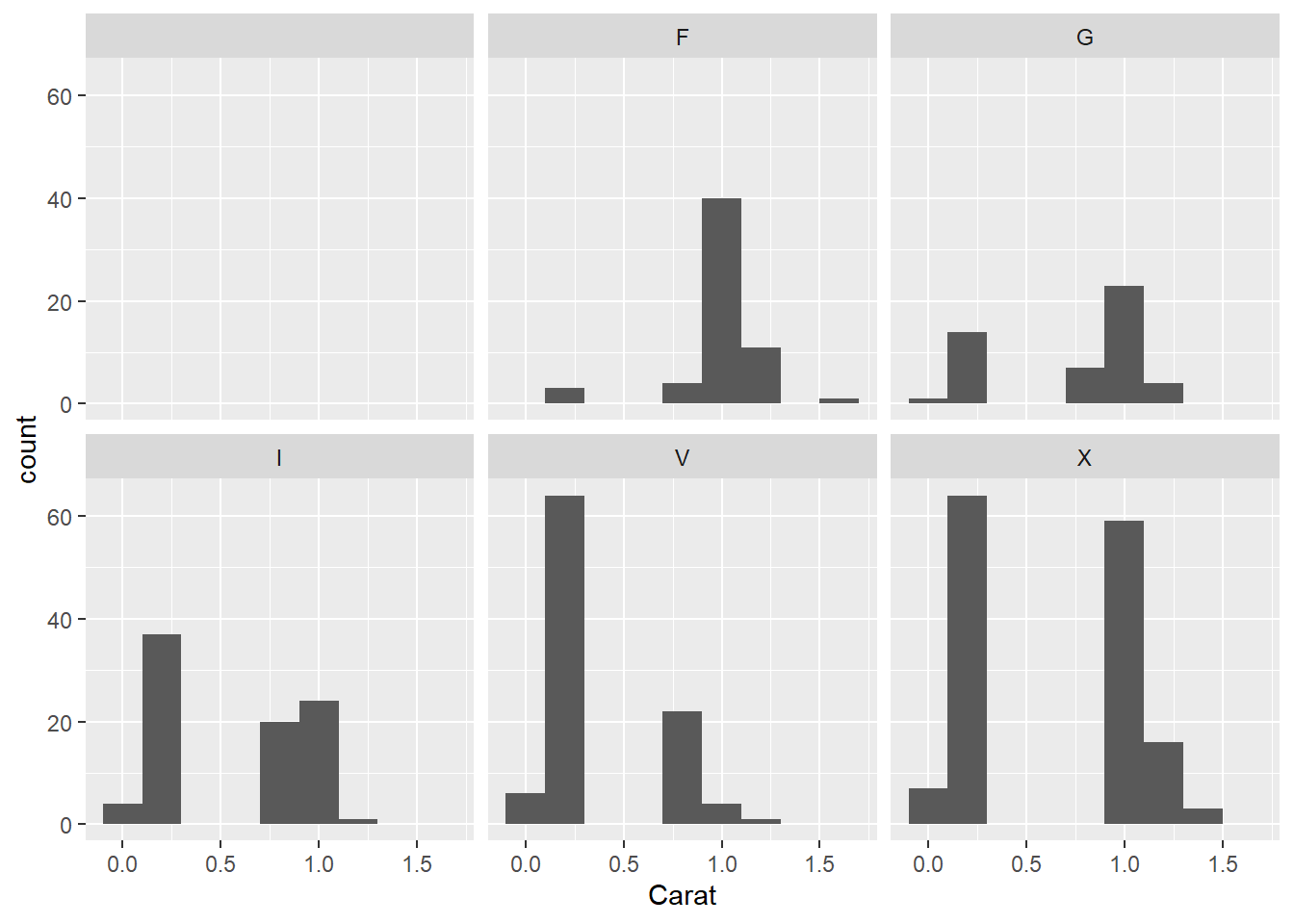

Variable correlated with cut:

Carat and cut have a negative correlation (see box plot below)- fair cuts are typically higher carat, while ideal cuts are typically lower carat. This could be due to the scarcity of larger diamonds, as well as the technical challenge of cutting a large stone into an ideal cut. This is also why lower quality diamonds, even if they are high carats, are more expensive.

diamonds %>%
  ggplot(aes(x=Cut,y=Carat, color=Cut)) +
  geom_boxplot()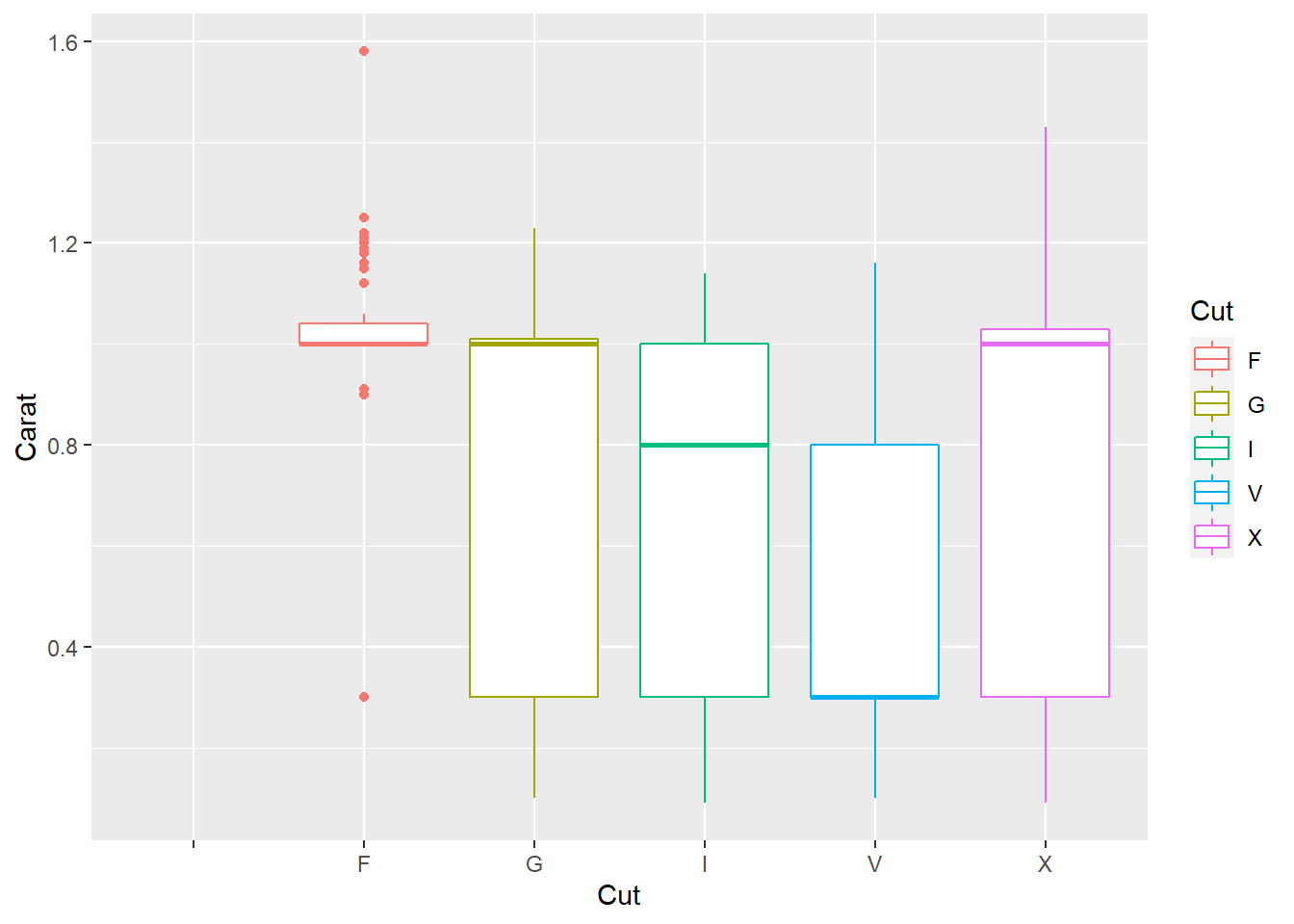

Predicting Diamond Price

To predict diamond price, we would first try to fit the data with a linear regression model.

QQ plot and histogram both show that variable price shows a better normality after log transformation

par(mfrow=c(1,2))
qqnorm((diamonds$Price),main="Normal Q-Q Plot of Price");qqline((diamonds$Price))
qqnorm(log(diamonds$Price),main="Normal Q-Q Plot of log Price");qqline(log(diamonds$Price))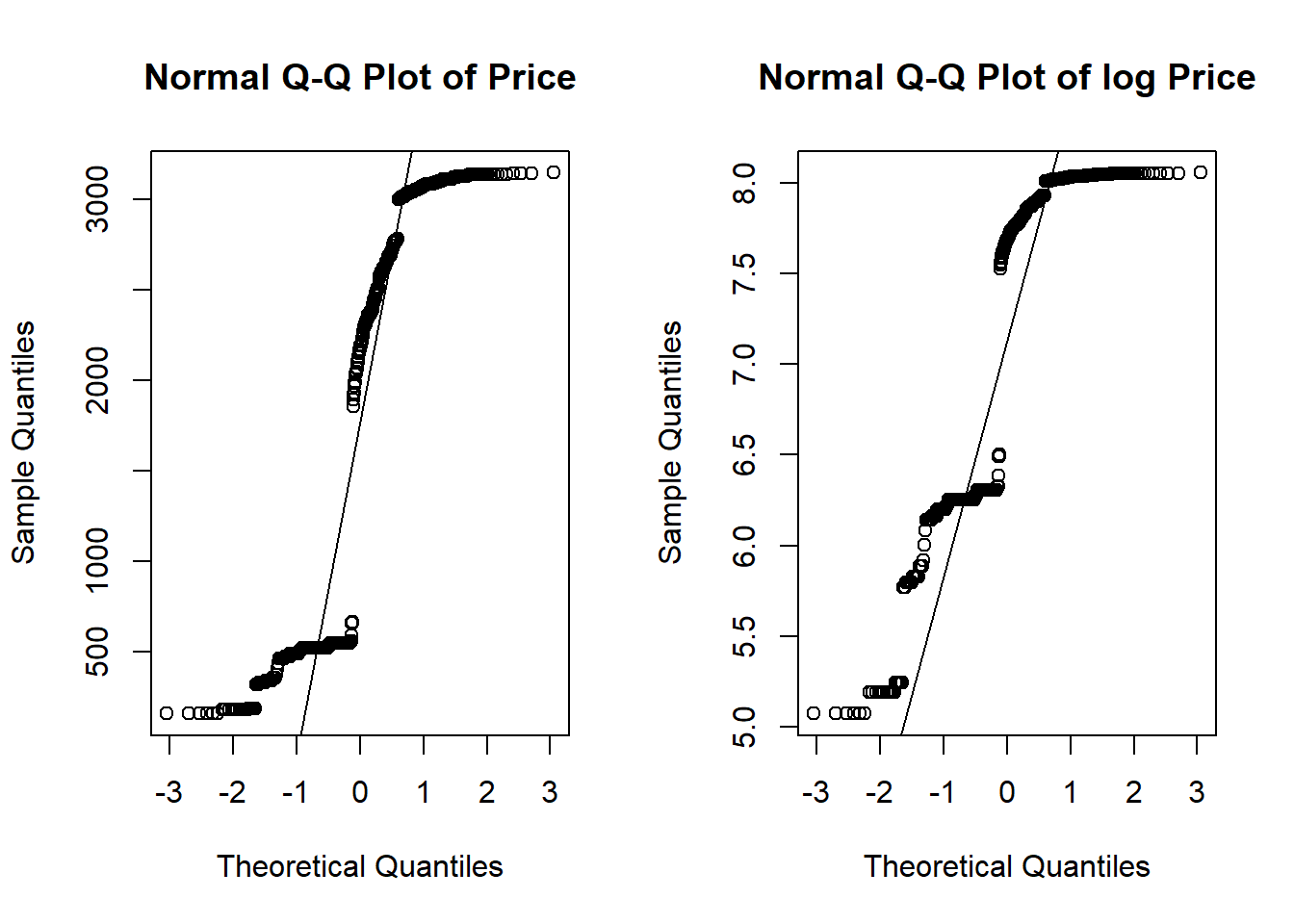

par(mfrow=c(1,2))
hist(diamonds$Price,main="Price")
hist(log(diamonds$Price),main="log Price")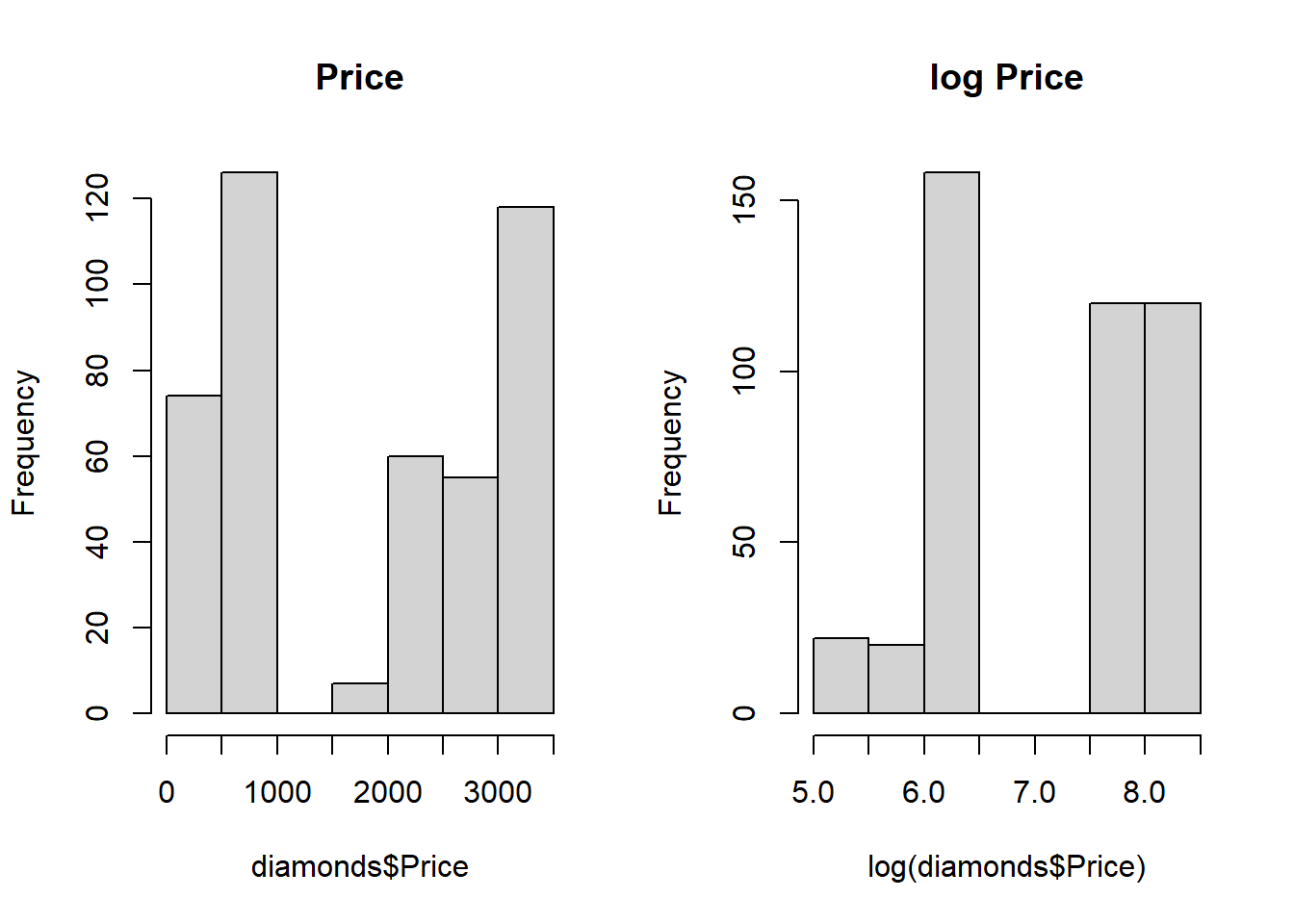

Linear Regression

We use the lm function to build the regression model, with the features that we have selected in earlier sessions.

lm1= lm(log(Price)~ log(Carat) + Cut+Colour+Clarity, data= diamonds)
summary(lm1)
## 
## Call:
## lm(formula = log(Price) ~ log(Carat) + Cut + Colour + Clarity, 
##     data = diamonds)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.31669 -0.08361 -0.03338  0.07873  0.83362 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.95244    0.03411 233.162  < 2e-16 ***
## log(Carat)   1.49210    0.01377 108.356  < 2e-16 ***
## CutG         0.02004    0.02676   0.749 0.454312    
## CutI         0.04213    0.02464   1.710 0.088033 .  
## CutV         0.03127    0.02524   1.239 0.215962    
## CutX         0.02768    0.02161   1.281 0.200816    
## ColourE     -0.02668    0.03545  -0.753 0.452045    
## ColourF     -0.11124    0.03516  -3.164 0.001671 ** 
## ColourG     -0.13064    0.03618  -3.611 0.000342 ***
## ColourH     -0.22083    0.03460  -6.382 4.65e-10 ***
## ColourI     -0.26298    0.03455  -7.611 1.82e-13 ***
## ColourJ     -0.35873    0.03544 -10.122  < 2e-16 ***
## ColourK     -0.39327    0.03996  -9.841  < 2e-16 ***
## ColourL     -0.44513    0.05044  -8.825  < 2e-16 ***
## ClarityI2   -0.19748    0.02940  -6.716 6.11e-11 ***
## ClaritySI1   0.37499    0.02641  14.200  < 2e-16 ***
## ClaritySI2   0.29185    0.02197  13.282  < 2e-16 ***
## ClaritySI3   0.09376    0.03107   3.018 0.002701 ** 
## ClarityVS1   0.51455    0.03576  14.389  < 2e-16 ***
## ClarityVS2   0.44413    0.03275  13.562  < 2e-16 ***
## ClarityVVS1  0.51225    0.10093   5.075 5.83e-07 ***
## ClarityVVS2  0.46022    0.06454   7.131 4.41e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1327 on 418 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.9811, Adjusted R-squared:  0.9801 
## F-statistic:  1032 on 21 and 418 DF,  p-value: < 2.2e-16

Compare with a model before log transformation:

lm2= lm(Price~Carat+Cut+Colour+Clarity, data= diamonds)
summary(lm2)
## 
## Call:
## lm(formula = Price ~ Carat + Cut + Colour + Clarity, data = diamonds)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -871.84 -113.74  -30.85  153.66  758.43 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1262.96      75.10 -16.817  < 2e-16 ***
## Carat        4021.16      47.87  84.007  < 2e-16 ***
## CutG          103.69      45.47   2.280 0.023083 *  
## CutI          190.10      41.93   4.533 7.59e-06 ***
## CutV          204.53      43.15   4.740 2.93e-06 ***
## CutX          150.08      36.85   4.073 5.54e-05 ***
## ColourE      -222.88      60.13  -3.707 0.000238 ***
## ColourF      -326.58      59.66  -5.474 7.59e-08 ***
## ColourG      -267.34      61.47  -4.349 1.72e-05 ***
## ColourH      -455.52      58.73  -7.756 6.75e-14 ***
## ColourI      -512.56      58.61  -8.746  < 2e-16 ***
## ColourJ      -729.74      60.22 -12.119  < 2e-16 ***
## ColourK     -1004.86      68.61 -14.645  < 2e-16 ***
## ColourL     -1138.90      86.13 -13.224  < 2e-16 ***
## ClarityI2    -593.78      50.17 -11.835  < 2e-16 ***
## ClaritySI1    955.49      46.18  20.691  < 2e-16 ***
## ClaritySI2    812.39      38.59  21.052  < 2e-16 ***
## ClaritySI3    236.55      52.83   4.477 9.77e-06 ***
## ClarityVS1   1187.11      61.77  19.219  < 2e-16 ***
## ClarityVS2   1039.77      56.81  18.304  < 2e-16 ***
## ClarityVVS1  1431.16     173.41   8.253 2.04e-15 ***
## ClarityVVS2  1031.59     111.48   9.254  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 225.5 on 418 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.965,  Adjusted R-squared:  0.9632 
## F-statistic: 548.5 on 21 and 418 DF,  p-value: < 2.2e-16

The results show that lm1 outperforms lm2; however, while lm2 is adequate, there is a risk of inaccurate estimates from lm2 due to its violation of the regression assumptions. Standardized beta coefficients can be used to determine which feature has the greatest impact on price prediction because the coefficients are all on the same scale:

lm.beta(lm1)
##  log(Carat)        CutG        CutI        CutV        CutX     ColourE 
##  1.14734123          NA          NA          NA  0.02128562          NA 
##     ColourF     ColourG     ColourH     ColourI     ColourJ     ColourK 
##          NA          NA -0.16980633          NA          NA          NA 
##     ColourL   ClarityI2  ClaritySI1  ClaritySI2  ClaritySI3  ClarityVS1 
## -0.34228223          NA          NA          NA  0.07209822          NA 
##  ClarityVS2 ClarityVVS1 ClarityVVS2 
##          NA          NA  0.35388233